present|Python+经济学：资本边际效率与IRR Python|现金流|经济学

文章图片

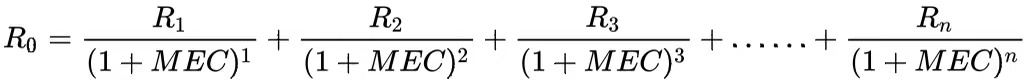
文章图片

前置知识：贴现与贴现率
由于投资不再是外生变量，因此在IS-LM模型的开篇，课本一般先引入资本边际效率（Marginal Efficiency of Capital ， MEC）这一概念来探讨投资规模的决定。

资本边际效率是一种贴现率，这种贴现率正好使一项资本品的使用期内各预期收益的现值之和等于资本品的供给价格或重置成本。

熟悉金融学的朋友们一定知道，贴现其实相当于利息的逆运算。假设银行一年期储蓄利率为5% ，那么100元存款一年的本利和为105元。如果反过来思考，假定银行利率5% ，一年之后可以获得105元的本利和，那么当前本金应为100元。这时，一年后的105元的现值（Present Value ， PV）为100元，而在现值求解中的利率称为贴现率（Discount Rate）。
例如，第n年获得的收益贴现到初期可以用以下公式：

借助这个公式，我们可以推出MEC的计算公式：

例如下面的例子：

某企业投资了30000元购买机器设备，机器使用年限为3年，三年后全部损耗，假定扣除了原材料、人工成本后各年的预期收益分别为11000元、12100元、13310元，合共预期收益为36410元，如果贴现率是10% ，那么该预期收益的现值正好与机器购买成本相等，此时10%即是资本边际效率MEC 。

如用式子表达则是：

在Python中，我们一般采用内部收益率（Internal Rate of Return ， IRR）函数来代表MEC ，因为从定义的角度出发，两者的描述基本一致：

内部收益率（Internal Rate of Return (IRR)），就是资金流入现值总额与资金流出现值总额相等、净现值等于零时的折现率。

但值得注意的是，由于模块更新，新的Numpy包中已不包含irr函数，需要安装numpy_financial包以获得金融计算支持。
这里用一道例题来做说明：

一笔投资为2850元，年利率为4% ，以后三年每年可以带来收入1000元，则这笔投资的资本边际效率（）年利率。
A.大于
B.小于
C.等于
D.不确定

代码实现：
import numpy_financial as npf
PresentValue = https://mparticle.uc.cn/api/0
Years = 3
#每年收益1000元
IncomePerYear = 1000
#题目提供的贴现利率
Interest_Rate = 0.04
#初始投资金额
Investment = 2850
#用于存放每年收益贴现值的列表
PVFlow = [

#用于存放每年现金流（含初始投资金额）的列表
CashFlow = [

##第一部分，计算每一年收益的折现值，并将其加总
#列表的第一个元素索引值是0 ，但贴现计算的分母指数从1开始，因此写作i+1
for i in range(0Years):
pvflow_i = IncomePerYear / (1+Interest_Rate)**(i+1)