j1|中科大何力新教授:当量子力学遇见AI——深度学习在超算平台上模拟量子多体问题( 五 )
另一个计算热点是SR优化方法。在SR算法中一个重要步骤是计算大的关联矩阵,然后求解线性方程组。具体哪部分的耗时是最严重的,其实是由模型参数大小所决定的。如果系统越大,采样越耗时,参数越多,SR方法的耗时越大。
文章插图
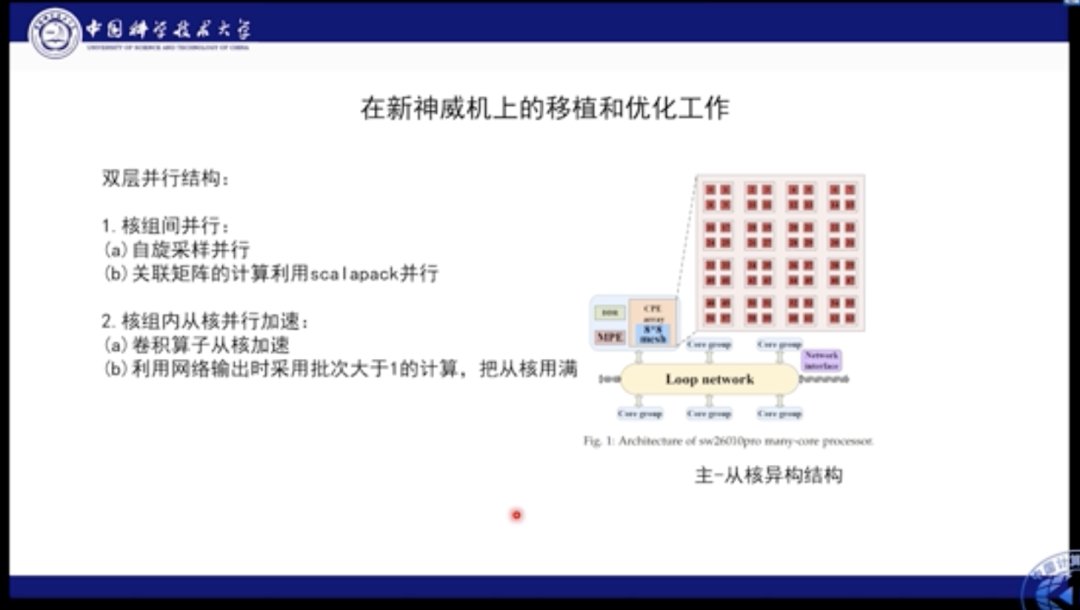
我们分别在自己的机器以及新一代的神威机上进行了验证和部署。神威机具有异构的结构,其NPI处于核组之间,因此有64个组合。在核组级别上的并行本质是线程并行。神威机的异构结构很适合此类应用,因此为了最大化利用神威机的能力,我们针对神威机的特点和应用特点设计了双层并行方案。首先在核组之间的并行被用作自旋采样,即每个自旋部署在不同的核组之上进行独立采样。在求解线性方程组的时候,会使用ScaLAPACK进行计算划分。在并行内部,我们使用卷积算子从核加速,并利用网络输出时采用批次>1的计算,将从核的计算性能妥善利用。
文章插图
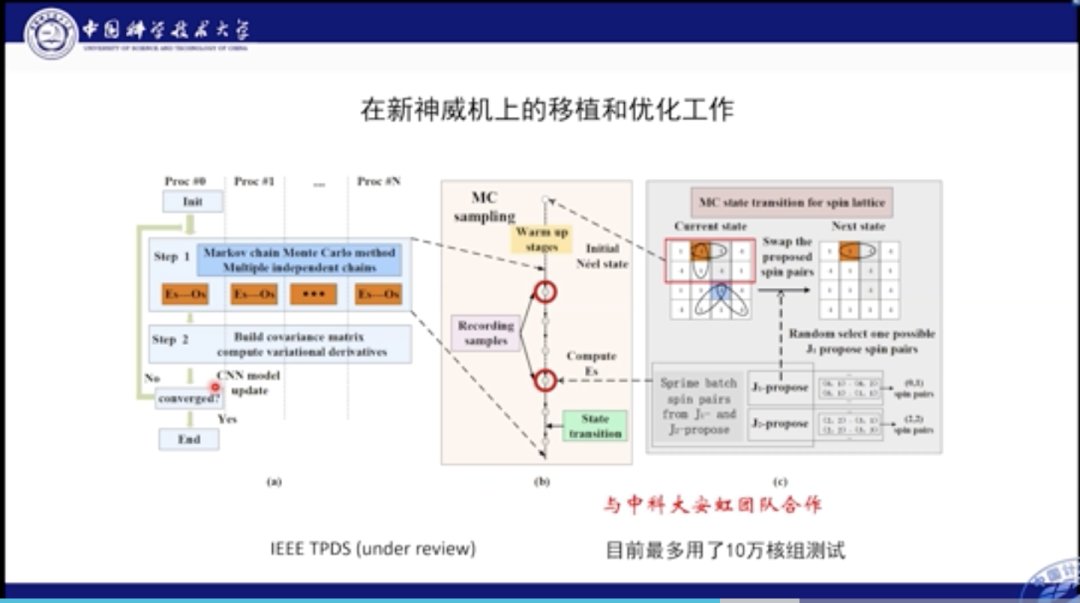
这是我们的程序在新的神威机上的移植和优化的示意图全览。可以看到在不同的核组之间我们进行了单独独立的采样;采样后将其收集并计算关联矩阵,并求导更新参数。这项工作最大利用了10万核组测试。
文章插图
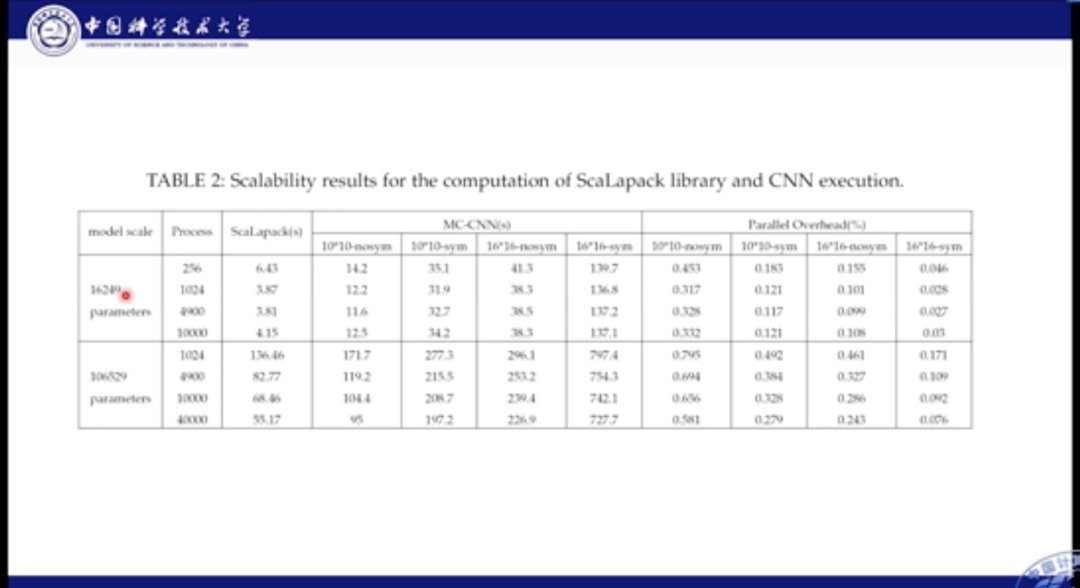
在性能表现方面,我们对比各个主机的用时结果。从上图中我们可以看到,我们分别比较了16000个参数,和10万个参数的场景。不论参数量如何,其主要的计算时间还是集中在前向计算部分,SR优化的占比只有1/4左右。
文章插图
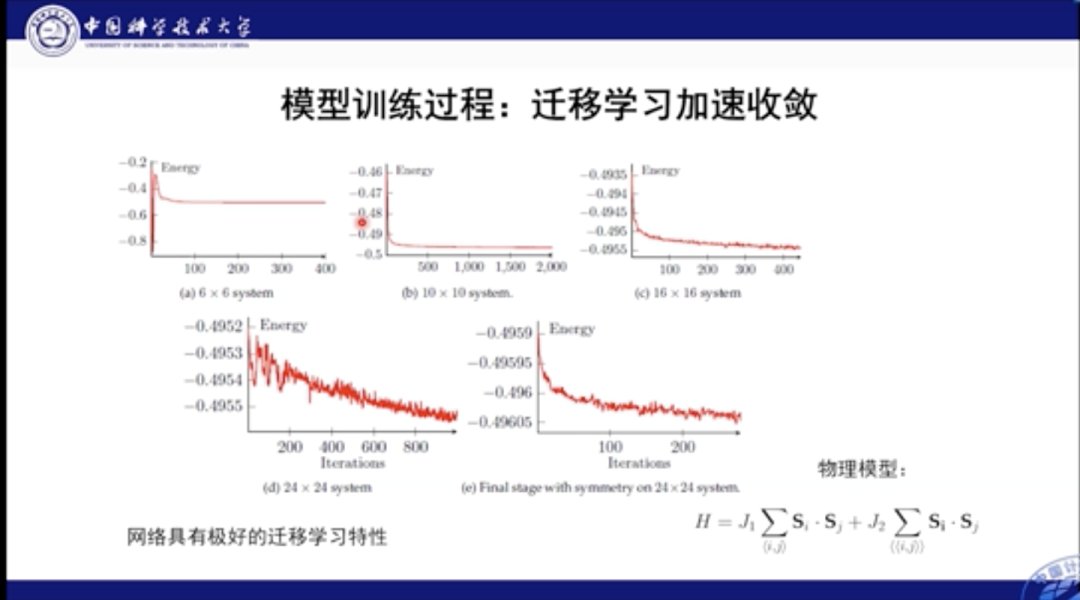
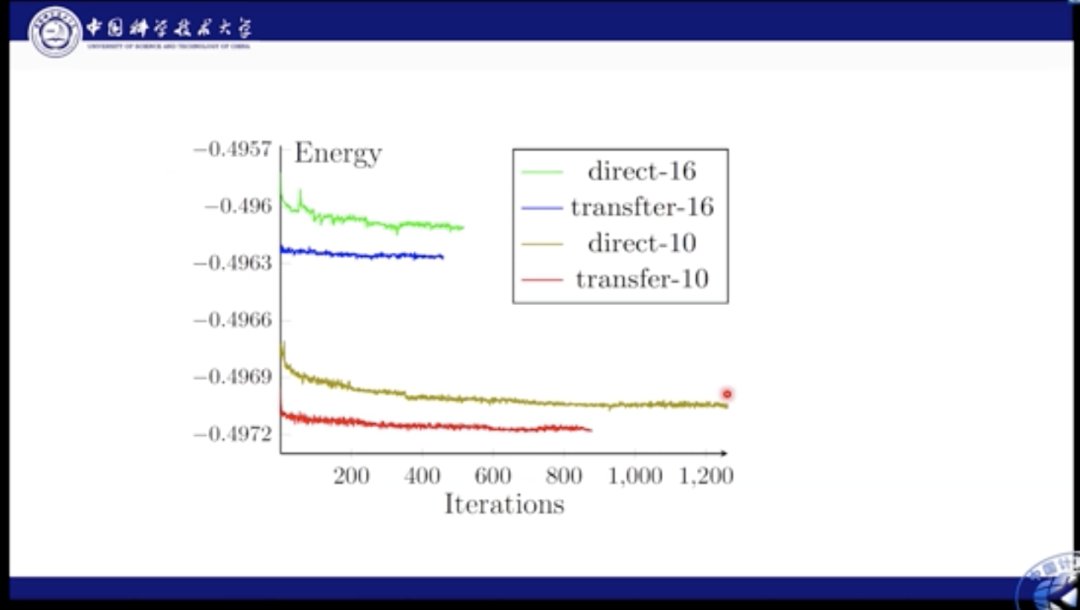
本工作的另一个优点在于其可迁移性极高。我们首先可以在较小的神经网络中进行学习,而后将其扩展到体积大的网络中。在实践中,迁移后通常只需要几百步便可以使大网络收敛,这无疑加速了模型的训练和应用。
文章插图
这里我们对比了性能。绿色和棕色线都是直接学习的结果,蓝色和红色是迁移的结果。通过图中结果我们知道,如果使用直接学习,则网络很难收敛到最佳结果,而迁移则极大加快了这个最优化的过程。

文章插图
文章插图
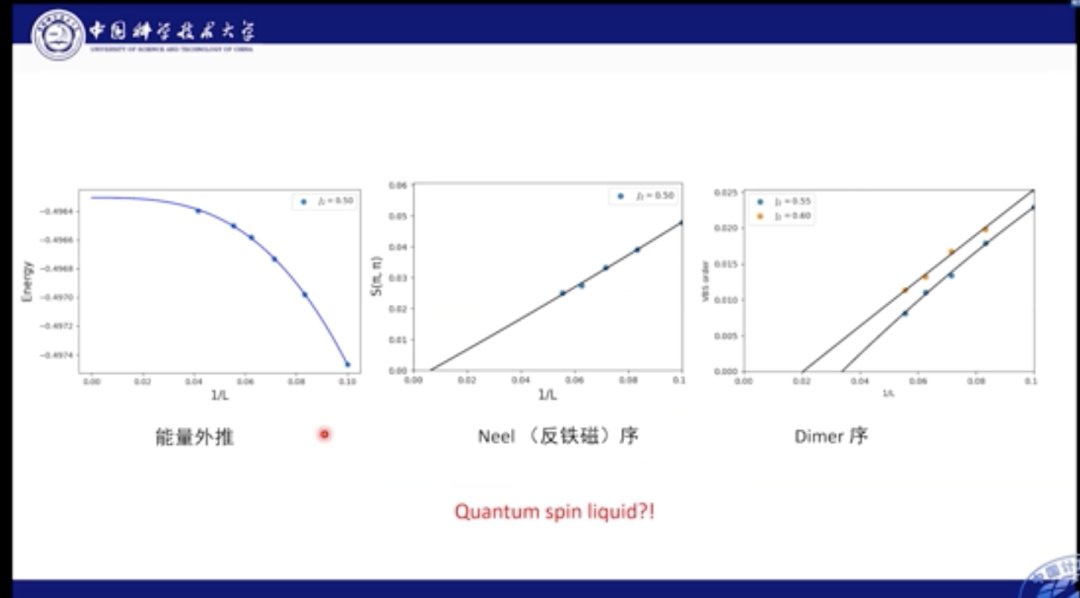
我们也分析了基态能量部分的外推结果,经过计算发现,能量在网格达到24×24后便逐渐收敛,我们也对多种磁序进行外推,比如Dimer序和反铁磁序。结果发现,系统在中间区域的基态是自旋液体相。
文章插图
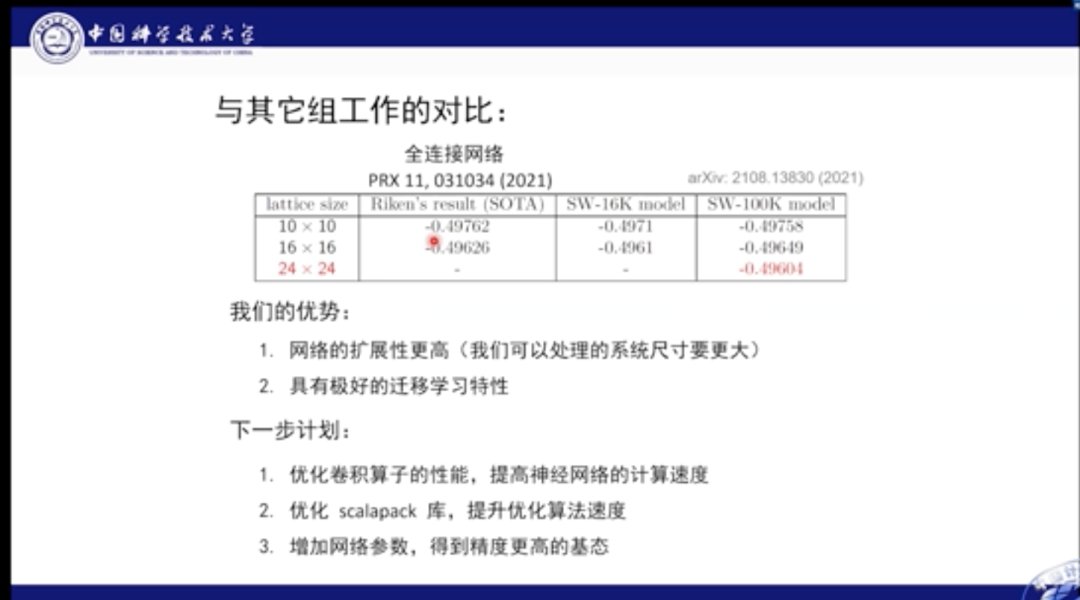
与之前的最佳结果对比,我们的优势在于,网络的扩展性更高,也就是可以处理的系统尺寸更大,具有极好的迁移学习特征。
在下一步工作中,我们将继续进行相关研究,主要优化卷积算子的性能,提高神经网络的计算速度;优化ScaLAPACK库,提升优化算法的速度;增加网络参数,得到精度更高的基态。
文章插图
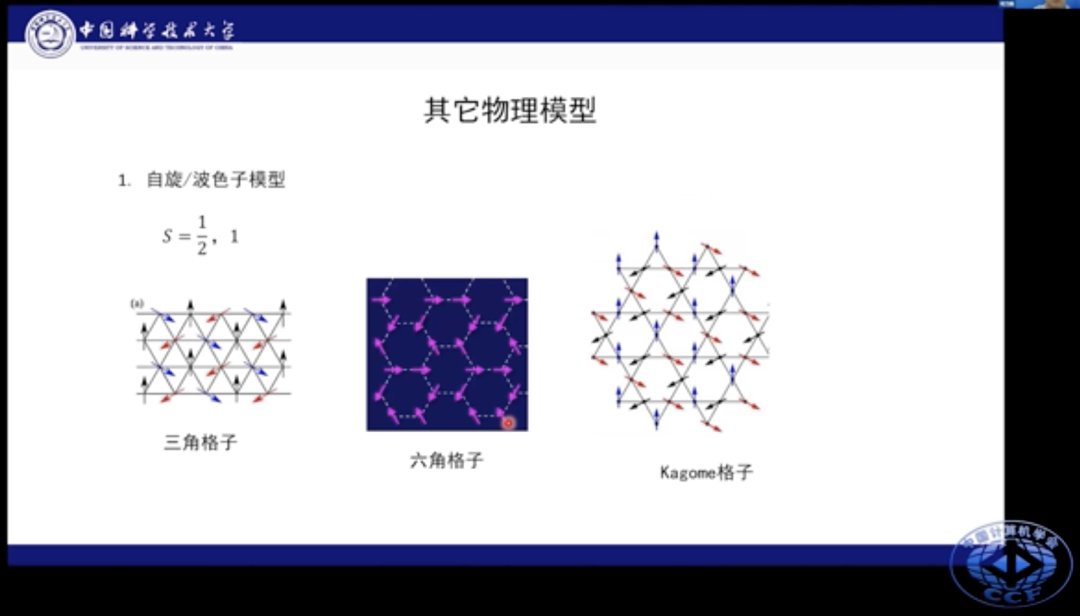
该模型可以进一步拓展到其他种类模型上,比如三角格子、六角格子和kagome格子等场景。我们还可以在近邻、次近邻作用的基础上添加次次近邻的相互作用。这些物理模型都有其特殊物理现象。
- 芯片|海归教授创办类脑芯片公司,即将全球首发量产,功耗可降低100-1000倍
- 中科大|华为任正非:“中国养的鸡,要回到中国的窝里下蛋!
- 百度百科|医生教授企业家等人物百度百科要怎么做,创建人物百度百科难吗
- 西工大张伟伟教授:智能流体力学研究的进展
- 华中科大|华为又迎来两位天才少年,来自俄罗斯00后,任正非:春天很快到来
- 福布斯|任正非要打车送教授,司机要130任正非只肯出100,司机转头开走了
- 任正非|任正非不顾高管反对,亲自开车接一位女教授,说:这是我的荣幸!
- 本文转自:澎湃新闻中国科学技术大学潘建伟团队首次实验证明实数无法完整描述标准量子力学|中科大潘建伟团队首次实验排除实数形式的标准量子力学
- 孔令贤|听了女教授3点建议,任正非放下身段向离职员工道歉:是公司错了
- 中医大学教授主讲望、闻、问、切四诊系统课程111讲免费领取学习
