悬铃木|谷歌量子计算团队再发Nature，或为容错量子计算机研发铺平道路( 二 ) 大会|2021世界机器人

改进的“悬铃木”处理器在硬件方面，研究人员基于“悬铃木”（Sycamore）处理器来实现量子纠错，它由一个二维的量子位阵列组成，其中每个量子比特可调谐地耦合到四个最近的邻域，即表面代码所需的连接性。
该处理器具有改进的读出电路设计，允许以更少的串扰进行更快的读出，并且每量子位的读出误差减少 2 倍，和它的前身一样，这个处理器有 54 个量子位，但研究人员最多使用了 21 个量子位，因为只有处理器的一个子集连接起来了。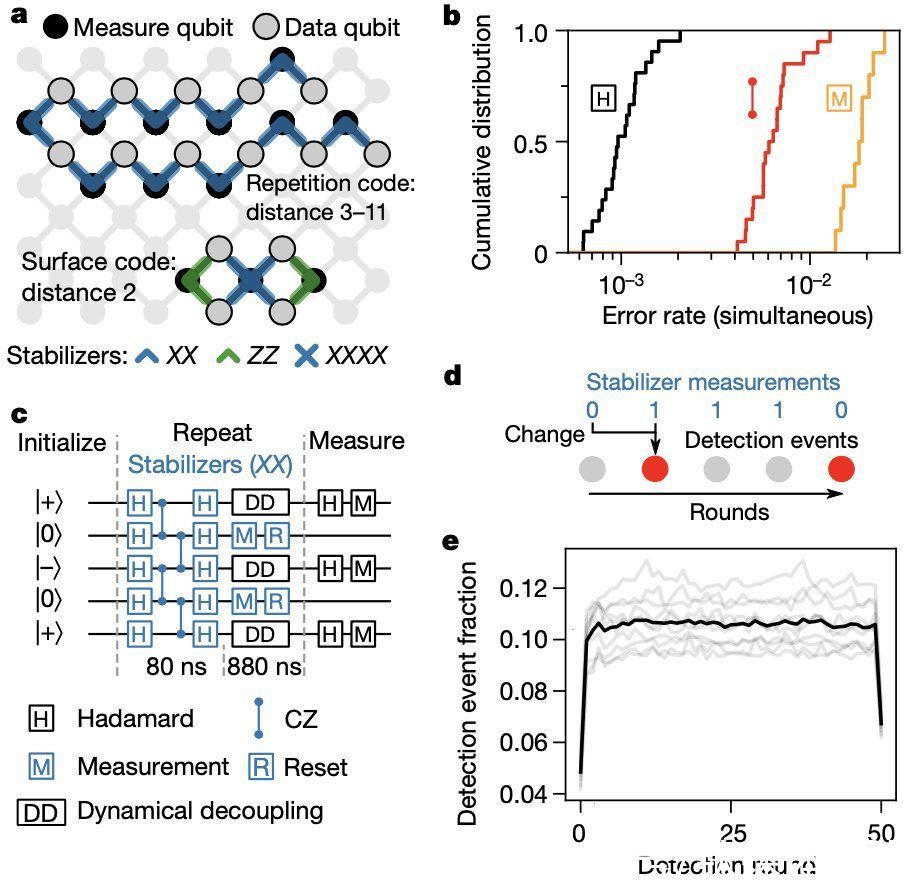

文章插图
图｜“悬铃木”上的稳定器电路概念图，构成稳定器电路的操作错误率以及相位翻转码电路示意图等（来源：Nature）
据论文描述，此次实验利用了“悬铃木”结构的门校准的最新进展。
首先，研究人员通过将每个量子位的频率扫过读出谐振器的频率，从激发态（包括非计算态）中移除布居。这种复位操作附加在量子纠错电路中的每次测量之后，并在 280ns 内产生误差低于 0.5% 的基态；
然后，他们利用两个量子位元的联合态（1，1）和（0，2）之间的直接交换来实现一个 26ns 受控 Z（CZ）门，可调量子比特-量子比特耦合允许这些CZ门以高并行度执行，并且在重复代码中同时执行多达10个CZ门；
最后，使用量子纠错的结果来校准每个 CZ 门的相位校正，同时利用交叉熵对标，结果发现发现 CZ 门泡利平均误差为 0.62%。
研究人员将重复码实验的重点放在位相翻转码上，在位相翻转码中，数据量子位占据了对能量弛豫和退相都很敏感的叠加态，这使得它的实现比位相翻转码更具挑战性，也更能预测表面码的性能。在测量和复位期间，数据量子位被动态解耦，以保护数据量子位免受各种退相源的影响。
研究人员分析实验数据的第一步是将测量结果转化为错误检测事件，即相邻回合之间相同测量量子位的测量结果变化，他们将检测事件的每个可能时空位置（即特定量子位和圆）称为检测节点，对于 50 轮 21 量子位相位翻转码中的每个检测节点，他们都绘制了在该节点上观察到检测事件的实验分数。
在第一轮和最后一轮检测中，检测事件的分数与其他轮相比有所降低。在这两个时间边界回合中，通过比较第一个稳定器测量和数据量子位初始化来发现检测事件。因此，在时间边界回合中的测量量子位读出期间，数据量子位不受消相干的影响，这说明了多回合运行量子纠错对准确基准性能的重要性。
除了这些边界效应，研究人员还观察到平均检测事件分数为 11%，并且在所有 50 轮实验中都是稳定的，这是量子纠错可行性的关键发现。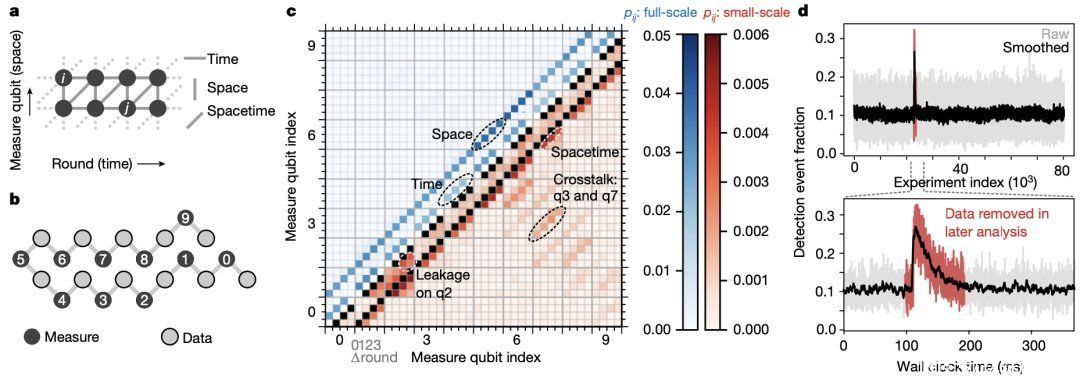

文章插图
图｜错误检测分析（来源：Nature）
接下来，研究人员描述了检测事件之间的成对相关性。通过计算任意一对检测节点之间的相关概率来检验“悬铃木”处理器是否符合期望，正如预期的那样，最明显的相关性要么是类空间的，要么是类时间的。
此外，他们还观察到一些偶发事件大大降低了重复代码的性能，未来通过改进设备设计或屏蔽来缓解这些事件，对于实现具有超导量子比特的大规模容错计算机至关重要。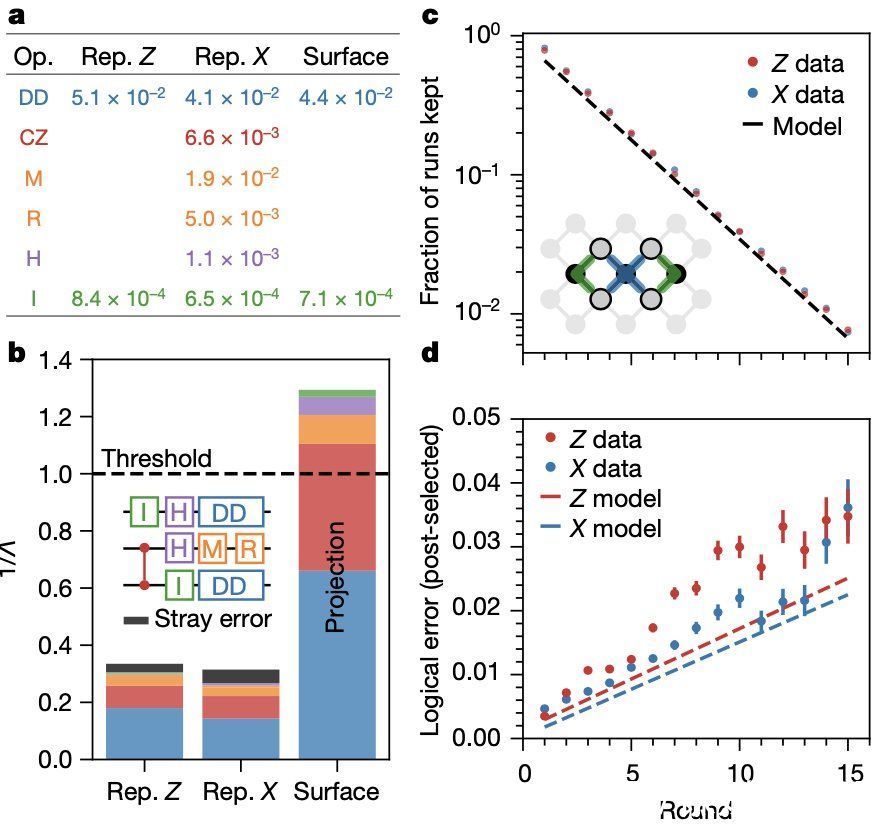

文章插图
图｜错误和表面码（来源：Nature）
重要的研究方向为了更好地理解本研究中的重复编码结果和设备的投影表面编码性能，研究人员用去极化噪声模型模拟了实验，这意味着在每次操作后都有可能注入随机泡利误差（X、Y 或 Z），使用平均错误率计算每种操作类型的泡利错误概率。总的来说，∧ 的测量值比模拟值差约 20%，研究人员将其归因于泄漏和串扰误差等机制，但未包括在模拟中。