|PyTorch常用5个抽样函数

PyTorch是一个开源的深度学习框架，它提供了一个用于高级特性的Python包。在本文中，我们将介绍PyTorch中的常见抽样函数。抽样是一个统计过程，它从总体中提取一个子集，通过子集来研究整个总体。
torch.bernoulli()伯努利分布是一个离散分布，有两个结果，即成功和失败。如果成功的概率是p ，那么失败的概率是(1-p) ，反之亦然。
PyTorch的实现和相应的输出如下:
a = torch.empty(3 3).uniform_(0 1)
print(a)
输出如下：
tensor([[0.0966 0.7385 0.6546

[0.4255 0.8294 0.8315

[0.8065 0.8228 0.6467

)
现在我们把bernoulli()函数应用到张量上
torch.bernoulli(a)
输出如下：
tensor([[0. 1. 1.

[1. 1. 0.

[1. 0. 1.

)
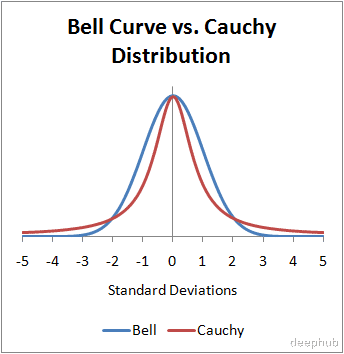
torch.Tensor.cauchy_()柯西分布，又称柯西-洛伦兹分布，在统计学中，具有两个参数的连续分布函数，最早于19世纪初由法国数学家奥古斯丁-路易斯·柯西研究。后来， 19世纪的荷兰物理学家亨德里克·洛伦兹(Hendrik Lorentz)用它来解释强迫共振或振动。第一眼看柯西分布看起来像正态分布，但它的“尾巴”并不像正态分布那样迅速逐渐消失。
柯西分布可能看起来类似于正态分布，它的峰值比高斯分布高，与正态分布不同的是，它的尾部衰减得更慢。

a = torch.ones(3 3)
a
输出：
tensor([[1. 1. 1.

[1. 1. 1.

[1. 1. 1.

)
现在我们应用cauchy_()函数
torch.Tensor.cauchy_(a)
输出：
tensor([[-4.5374 0.3726 0.4947

[ 0.4111 0.9167 0.7214

[ 1.0533 -9.2247 0.7620

)
注意，这里的函数名称以\"_\"结尾，这是pytorch的一个规定，他将会用改写参数，也就是我们传进去的变量a
torch.poisson ()泊松分布用于计算一个事件在平均价值率(时间)的一定时间内发生的可能性。泊松分布是一个离散的概率分布。
a = torch.rand(4 4) * 5 # rate parameter between 0 and 5
torch.poisson(a)
输出如下：
tensor([[2. 1. 0. 8.

[2. 3. 3. 3.

[0. 0. 1. 6.

[0. 5. 3. 3.

)
torch.normal ()正态分布，又称高斯分布，是独立随机变量的连续分布函数。该分布有一个钟形曲线，其特征有两个参数:均值，即图型上的最大值，图总是对称的;还有标准差，它决定了离均值的差值。
【|PyTorch常用5个抽样函数】torch.normal(mean=torch.arange(1. 11.) std=torch.arange(1 0 -0.1))
输出如下：
tensor([-0.6932 2.3833 2.3547 3.8103 5.4436 5.8295 7.5898 8.4793
9.1938 10.0637
)
torch.rand ()PyTorch torch.randn()返回一个由可变参数大小(定义输出张量形状的整数序列)定义的张量，包含来自标准正态分布的随机数。
标准正态分布，也称为z分布，是一种特殊的正态分布，其均值为0 ，标准差为1
torch.randn(44)
输出如下：
tensor([[-1.3119 -0.2177 -0.2496 0.2361

[-1.2755 -0.2271 1.5297 0.6433

[-0.4198 -0.9269 -0.6260 -0.9713

[ 0.6730 -1.2400 2.1338 0.2051

)
https://avoid.overfit.cn/post/17413e750e7e404e9f8714c1eeb06dc4