函数|LTV预估与留存曲线拟合：指数函数还是幂函数？( 二 ) 合成|高通量|生物|合成生物学

某些情况下，对两个指数函数线性组合后的曲线，拟合度更高的（即R方更大的），却不再是指数函数了，而是幂函数！
这个有意思的现象，各位有兴趣的话，可以自行验证一下。
五、遗忘曲线与留存曲线关于遗忘曲线的结论，对我们理解留存曲线有什么帮助吗？
事实上我们早就发现，这两个曲线惊人地一致。
如果把拉新激活的动作视为最初始的记忆训练，那么在后续的时间里，如果没有再次激活，用户就会以一定的概率，自然而然地遗忘我们的App，表现就和遗忘曲线是一样的。
为了让用户回到我们的App，提升用户留存率，我们通过各种push召回它们，这也和关于记忆的研究中，定期复习的方法如出一辙。
同时，和混杂材料带来的遗忘曲线类似，绝大多数功能丰富的成熟应用，留存曲线都应该是衰减程度更慢的幂函数。
事实上也确实如此，包括前面提到的番茄小说例子在内，我从QuestMobile验证了其他一些常见App，以及手头有的一些内部数据，它们的留存曲线的确都是拟合成了幂函数：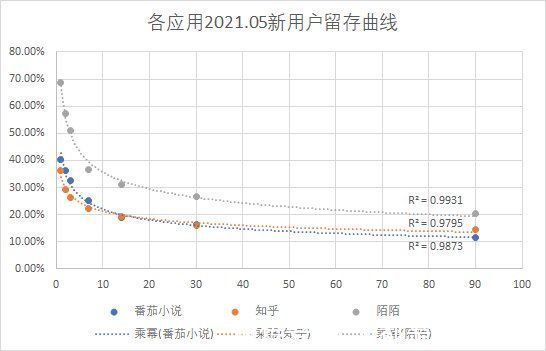

文章插图
番茄小说、知乎与陌陌2021.05新用户留存数据，QuestMobile
六、对数函数与其他LTV预估方法最后再补充两个点。
在前面的趋势线拟合中，有一个对数函数可能会是迷惑选项。
对数函数的表达式是：
随着t的增长，对数函数计算得到的结果很可能会小于0，而不是像指数函数和幂函数一样始终保持大于0的结果。
小于0的留存率是没有意义的，因此如果最优拟合的结果是对数函数，更可能的情况是巧合或者样本量太小，对数函数在这个场景下本身没有合理的物理意义。
不妨在指数函数或者幂函数中选择一个，他们的拟合度离最优拟合应该差不了多少。
而对于最开始提到的LTV预估公式：
需要说明的是，这里面隐藏了一个假设：ARPU值恒定不变，是个常数。
但在现实情况下，这样的假设往往会带来一些误差，因为随着留存时间增加，这部分用户的ARPU总是会随之有所变化。
一种调整的方法是对ARPU同样进行预估，将公式改造为：
不过ARPU的变化规律可能很难找，或者压根就没有像留存曲线这样简单清晰的规律。
因此另一种调整方法是不做拆分，用更多样本数据和特征数据，整体地对用户贡献价值进行函数拟合预估：
这样的方法需要足够多的样本，本身也更适合需要精细化的运营场景，这里就不再展开了。
参考资料：
[1] https://supermemo.guru/wiki/Exponential_nature_of_forgetting
[2] https://supermemo.guru/wiki/Forgetting_curve
作者：青十五；公众号：青十五，新书《策略产品经理：模型与方法论》作者
本文由 @青十五原创发布于人人都是产品经理，未经作者许可，禁止转载。
【函数|LTV预估与留存曲线拟合：指数函数还是幂函数？】题图来自Unsplash，基于CC0协议。