台积电|曲线缝合密度图英伟达|GPU|it芯片

文章图片

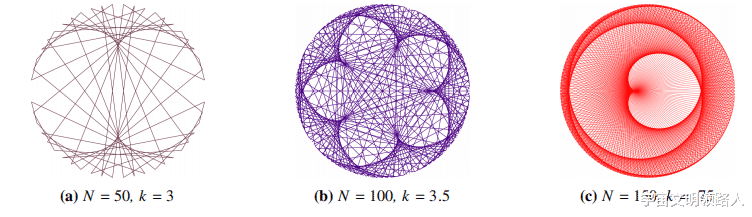
文章图片

文章图片

文章图片

女士们，先生们，老少爷们儿们！在下张大少。
曲线缝合是一种数学艺术风格，在这种风格中，直线的包络形成了突现的曲线。几乎不费吹灰之力，曲线拼接就可以在计算机程序中实现，可以很容易地对参数进行操作。计算机程序的灵活性和力量揭示了本身就很有趣的色彩层次。本文讨论了一种算法，这种算法不是将曲线拼接图案呈现为线段的集合，而是呈现为密度图。这些密度图允许对颜色层次进行探索，并引入了一种新的方法来呈现曲线缝合图像的新方法。
基本曲线缝合
曲线缝合是玛丽·埃佛勒斯·布尔(Mary Everest Boole)在19世纪发明的，当时她拿着用来画画的卡片，不是在上面画画，而是用缝纫针在图案的边缘打孔，把线从小孔中抽出来，形成线条。她最终发现了一些模式，使相交的线能创造出 \"由每条直丝线的一小部分组成的对称曲线\" [1
。人们仍然在创造曲线缝合作品，作为数学教育课程的一部分，作为一种爱好，也作为艺术。这些作品的创作方法是玛丽·布尔的原始方法，以及手绘和计算机生成的图像。

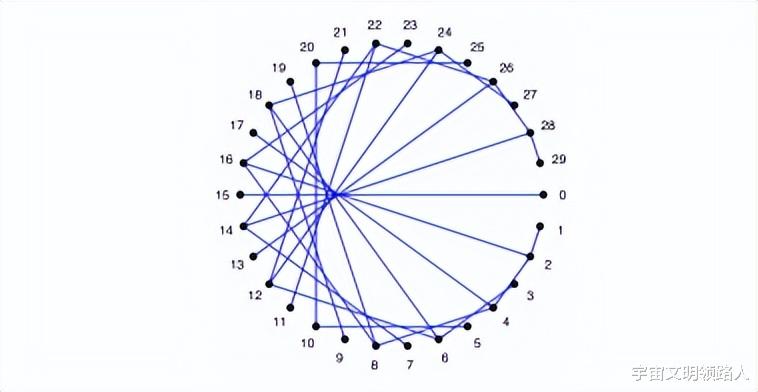
图1：N=30 ， k=2 。
【台积电|曲线缝合密度图】
图2:基础曲线缝合算法
曲线缝合的过程一般可以认为是沿着一套或多套路径定义了一组点P 。然后用一个映射函数f (i)将每个点pi∈P映射到pf (i) ，其中pf (i)也∈P 。然后，每一对点{pi pf (i)都作为一个线段的端点。当线段被画出来的时候，它们的包络线就会产生新的曲线和图案。在本文中，路径仅限于封闭的曲线，例如，圆、玫瑰曲线、环状线等等。
映射函数的常见定义是f(I)=(k?i)mod N ，其中N是P中的点的数量， k是一些整数值，如2 ， 3 ，等等。使用这个定义，图1说明了N=30和k=2时圆的结果。在实现曲线缝合算法时，使用曲线的参数方程g(θ)很方便，它可以从角度θi计算出点pi 。在这种情况下， f (i)被转化为f (θ) = k ? θ 。改变参数方程的方法并不改变最终的图像，因此大多数程序实现了图2所示的基本曲线缝合算法的变体。

图3：使用基本算法时N和k的影响
当在计算机程序中实现时，基本算法能够快速和容易地操作N和k 。它很容易使k的值（在手工制作曲线缝合工程时往往是低整数值）成为任意实数、整数或浮点数。图3说明了当基本算法应用于一个圆时可能出现的许多变化中的三个。
密度图
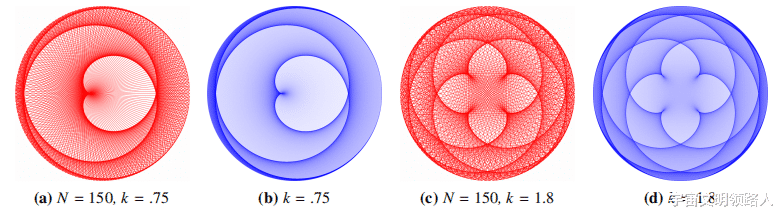
如图3(c)所示，随着基本算法给定的N值越来越高，整个图像中不同密度的线条开始导致颜色渐变。在线条交叉点较多且线段较近的区域，这些区域的整体颜色较深且较浓。在交叉点较少且线段相距较远的区域，这些区域的整体颜色较浅且不强烈。当我用基本算法逐步探索更复杂的图像时，我对颜色渐变的潜力更感兴趣，然后努力开发一种算法，强调渐变而不显示任何可见的线条。

图4：曲线缝合密度图算法
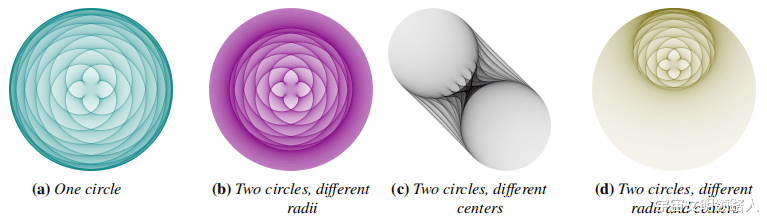
由此产生的曲线缝合密度图算法，如图4所示，是一种抽样算法。与基本算法不同的是，密度图算法从无限多的可能线段中计算出S条随机线段，以生成出现的曲线。从这些样本中，它选择一个随机点，其位置用于增加矩阵M中的密度计数。在生成所需数量的样本后，矩阵将包含代表最终图像中每个位置的线条密度的计数。