物理课|《张朝阳的物理课》继续讨论热力学初谈熵概念( 二 ) 小巨人|余建平|新材料|阿里云

文章插图
（张朝阳介绍热力学第二定律）
卡诺定理：高温低温热源确定，可逆热机效率最高
此前，张朝阳介绍过卡诺循环，他继续研究以卡诺循环工作的热机的效率。他说，“卡诺循环的每个过程都是准静态过程，是个可逆过程，利用卡诺循环从高温热源吸热来对外做功的热机是可逆热机。”卡诺定理指出，相同的高温热源和相同的低温热源之间，工作的一切不可逆热机的效率,都不能大于可逆热机。其中，热机的效率是指热机对外做的有用功W与它从高温热源吸收的热量Q的比值：

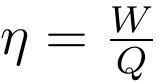
文章插图
“利用热力学第二定律可以证明卡诺定理。”张朝阳继续解释，首先考虑两个热机A与热机B，假设它们从高温热源吸热都为Q1，但对外做的功分别为W和W'，则它们的效率分别为：

文章插图
他提醒网友，假设热机A是可逆热机，若要利用反证法证明卡诺定理，就需要先假设其不成立，即ηA<ηB，那么有W'>W。为了说明此假设违反热力学第二定律，让热机A与热机B共用相同的高温热源T1与低温热源T2。由于A是可逆热机，而W'又比W大，于是可以用B所做的功W'的一部分推动A反向进行，这时候A向高温热源放出热量Q1，而因为B也从高温热源吸收热量Q1，于是这个过程中高温热源不变。再根据热力学第一定律，B给低温热源放出的热量是Q1-W'，A吸收低温热源的热量是Q1-W，于是整个过程相当于所有热机向低温热源吸收了Q1-W-(Q1-W')=W'-W>0的能量。而联合循环终了时，两热机的工作物质都恢复了原状，并且高温热源也没有变化，相当于热机从单一热源吸收W'-W>0的热量使之完全变成有用功而不引起其它变化，这违背了热力学第二定律的开尔文表述。所以最开始的假设ηA

文章插图
（利用热力学第二定律证明卡诺定理）
状态函数熵：从热机效率看宏观表达，从统计数目看微观意义
张朝阳进一步解释，假设前述的热机B同热机A一样也是可逆热机，那么根据卡诺定理可以得到ηA≤ηB，结合已经证明的ηA≥ηB，就可以得到ηA=ηB。“这说明，工作于两个一定温度的热源之间的可逆热机，其效率相等。”他提醒网友，“这同时也表明可逆热机的效率与具体的工作物质无关，那么效率只能由热源决定，而热源最基本的特征是温度，因此效率只是温度的函数。”假设热机从高温热源T1吸热Q1，给低温热源T2放热Q2，由热力学第一定律可知有用功为Q1-Q2，那么热机效率可以写成：

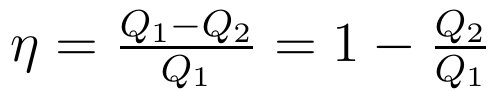
文章插图
而由于效率只是温度的函数，又可以得到：

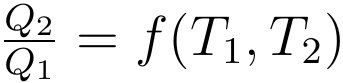
文章插图
接下来，张朝阳以理想气体作为热机工作物质为例，推导f的形式。从他的推导可见，从高温热源T1吸热的过程为a到b，体积从Va膨胀到Vb，由热力学第二定律可知，一个微小的过程吸收的热量为 ?Q=dU+pdV，而上节课也知内能只是温度T1的函数，在这个等温过程中dU=0，那么理想气体从高温热源吸收的热量Q1为：

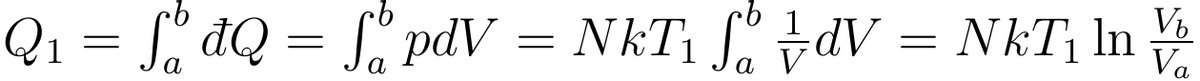
文章插图
理想气体与低温热源T2接触放出热量的过程为图中的c到d，体积从Vc减小到Vd，同理可以计算得到向低温热源放出的热量Q2为：

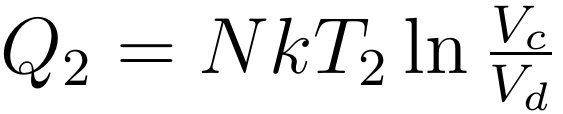
物理课|《张朝阳的物理课》继续讨论热力学 初谈熵概念( 二 )

物理课|《张朝阳的物理课》继续讨论热力学初谈熵概念( 二 )