张朝阳|学物理也要用到基础数学《张朝阳的物理课》推导球坐标系体积元( 二 ) 参数|智能|wi-fi|车型|永磁同步

同理，将x，y，z换成速度Vx，Vy，Vz，速度区间所示的体积微元dVxdVydVz对应到球坐标系里的体积微元就是V^2sinθdθdφdV，其中V是速率。所以当速率趋于零时，体积元以V^2方式减小到零，这就解释了为什么速率趋于零时对应的速率分布值也趋于零。
分割、换元、组合、等效：计算均匀球体的引力
作为球坐标系的一个典型应用，现在计算质量为m的质点与半径为r的球壳之间的引力，质点与球心的距离为R，具体参数如下图所示：

文章插图
（张朝阳巧妙选取积分变量计算球壳与质点的引力）
张朝阳继续说明，“设球壳密度为ρ，半径为r的球壳上的小体积元质量为ρr^2sinθdθdφdr，其与质点的距离设为l，则球壳与质点m之间的引力为：”

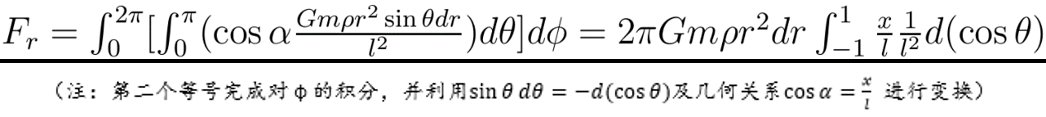
文章插图
如果将x与l表示为cosθ的函数，积分会变得比较难，故尝试选取其它参量作为积分变量。注意到cosθ可由其所在的直角三角形的边长表示为：

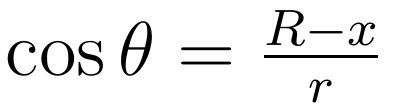
文章插图
那么质点m与球壳之间的引力为：

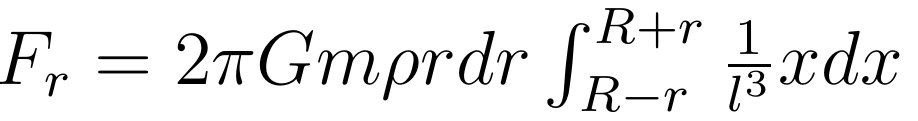
文章插图
现在只剩下x与l两个参量，只要将其中一个表示成另一个，就可以做积分。张朝阳选择将x用l表示出来，最终全部化成对l的积分。为了完成此目的，注意到包含θ所在的直角三角形有勾股定理：

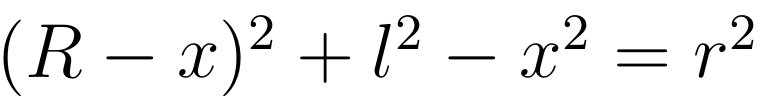
文章插图
利用此公式可以将x表示为：

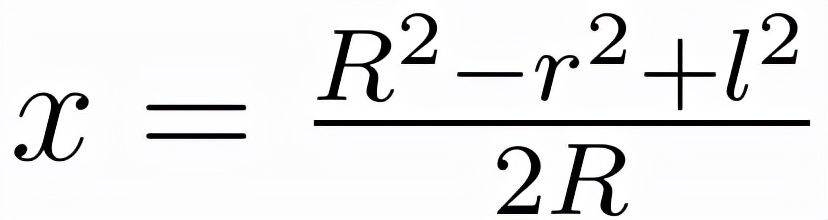
文章插图
最后代入积分公式里并完成对l的积分后：

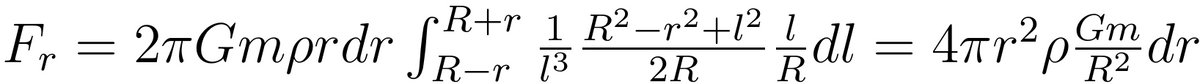
文章插图
注意到球壳的质量为4πr^2ρdr，R是质点到球壳的距离，从上述引力的公式可以发现，质点m与球壳的引力可以等效地看成是球壳所有质量集中在球心的引力。那么将球壳按照r积分起来，就得到质点m与球体之间的引力：

文章插图
他指出，“可以发现，质点与球体的引力也可以等效地把球体质量看成集中在球心，并且即使球体密度与径向距离有关，也不影响此结论。”
“球体在宇宙学里是普遍存在的形状，可以利用这个结论方便简易地得到其万有引力，所以这个结论具有非常重要的意义。”直播结尾，张朝阳告诉网友。
打造知识直播平台：搜狐视频发力价值直播吸引诸多科普播主入驻
截至目前，《张朝阳的物理课》已直播三十期。张朝阳先是从经典物理学开始，科普了牛顿运动定律与能量动量守恒；讲解机械振动与波动方程并计算空气中的声速，顺便讨论与此相关的理想气体状态方程和能量均分定理。尔后从经典物理的“两朵乌云”说起，向近现代物理过渡，包括由黑体辐射研究引出的维恩、瑞利-金斯、斯特潘、普朗克等系列公式；由电磁学和时空性质引发的相对论议题，如洛伦兹变换、尺缩钟慢、质能关系、粒子衰变等。
此后逐步进入量子力学领域，从基础的薛定谔方程、算符对易关系、不确定性原理等理论内容，到无限深势阱、氢原子波函数、原子能级与简并等基础模型，再到谐振子量子化、分子振转光谱、自由度的冻结、气体定容比热的温度阶梯等更加具体实用的案例。内容丰富、覆盖广泛，理论公式由浅入深、繁简交融，研究对象由小到大、由少到多，从单电子原子到多电子原子、多原子分子，再到由众多粒子组成的宏观物质，实际上已经逐渐进入到统计物理学领域。接下来的玻尔兹曼分布、麦克斯韦速度分布律等，也就顺势引入，顺理成章。