双原子|《张朝阳的物理课》气体比热随温而变？探究双原子分子比热问题( 二 )

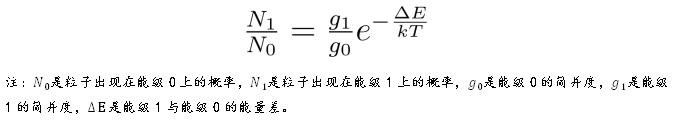
文章插图
若能级0为基态，由于能级能量在e指数上而且为负，粒子出现在某激发能级上的概率，随该能级能量的升高而快速下降。为了分析在室温下粒子处在激发态上的概率大小，张朝阳将kT用波数表示出来大约为200/cm，如果要激发的自由度的能量?E对应的波数比这个大得多，那么出现在这个自由度对应的激发能级上的概率将会非常小，分配到这部分自由度的能量将明显减少，不再像能量均分定理所说的那样平均分配。
张朝阳以一氧化碳为例，根据双原子分子转动能级角动量公式，激发其转动能对应的特征波数B大约为2/cm，比室温下的kT对应的波数要小得多，于是其转动能可以被比较完整地激发，满足能量均分定理。但激发一氧化碳振动能所对应的波数则远远大于室温下kT对应的波数，按照玻尔兹曼分布公式，粒子处在振动能激发态的概率会非常小，几乎都处于基态，其振动自由度被冻结，所以计算比热时可以忽略振动部分的2个自由度，从而室温下的比热的实验测定值就是5/2R。
经过推导分析，不难理解比热随温度的阶梯性质。张朝阳解释，当温度较低时，kT较小，只有三个自由度的质心平动能可以被完整激发，对应的比热是3/2R。温度增大时，kT逐渐变大，粒子出现在转动能激发态上的概率增加，越来越多的能量可以分配到转动能上，2个转动自由度冻结解除，得到的比热就是5/2R。当温度继续升高，以至kT可以与振动能相比拟时，出现在振动激发态上的概率增大，最终振动能自由度也可以贡献比热，最终得到的比热为7/2R。这就解释了比热随温度呈现阶梯状，以及各平台对应的比热值。
统计方法计算振动热容：粒子指数布居能级简并度相同
“除了能量均分定理可以计算比热，我们还可以通过玻尔兹曼分布与量子力学能级计算比热。”张朝阳继续推导，由于振动能级非常简单，我们以双原子分子理想气体为例，计算其振动自由度对应的比热。气体分子能量服从玻尔兹曼分布，分子处在不同能级的概率为：

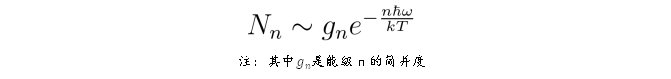
文章插图
那么，双原子分子理想气体中，单个分子的能量期望值为：

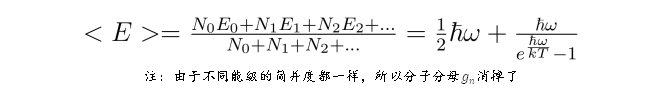
文章插图
在温度较高，kT>>?ω 时，上述能量可以按照?ω/（kT）展开：

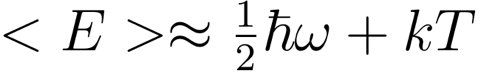
文章插图
可以求得振动自由度贡献的比热为：

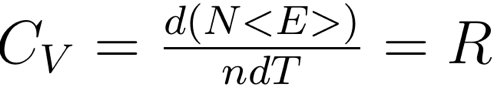
文章插图
这与能量均分定理求得的2个振动自由度贡献的比热结果2*1/2 R一致，也与定容比热随温度升高的阶梯图平台值一致。

文章插图
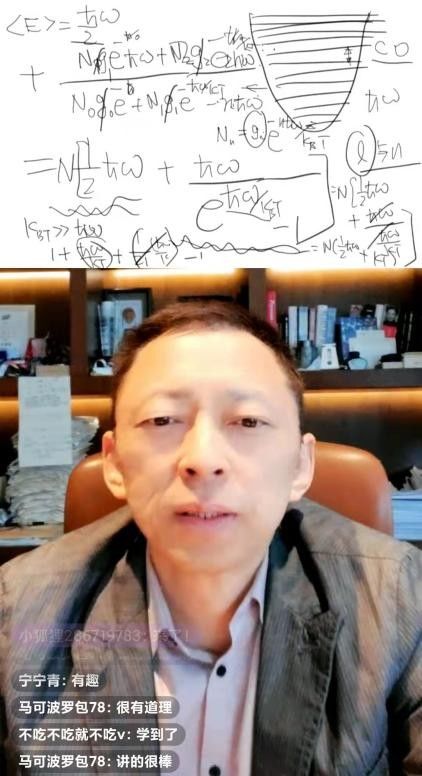
（张朝阳用玻尔兹曼分布推导分子振动能量）
打造知识直播平台：搜狐视频发力价值直播吸引诸多科普播主入驻
截止目前，《张朝阳的物理课》已直播二十多期。在第一、二课中，张朝阳科普了“力”和“速度”，算出马斯克的飞船和中国空间站每日绕地飞行圈数；第三、四课和“振动”相关，科普可见光的基本知识；第五、六课引发了关于音速和温度的大讨论；在第七、八、九课重温经典物理学的两朵乌云。
第十、十一课重点回顾黑体辐射曲线及其应用；第十二、十三、十四课尝试进入爱因斯坦的思想世界，推导出著名的公式“E=mc2”，并论证钟慢尺缩效应；第十五课讲解了原子的结构和原子核的衰变；第十六课开始进入量子力学，讨论光的波粒二象性、康普顿散射、海森堡不确定性原理，以及薛定谔方程等。