薛定谔方程|《张朝阳的物理课》探究谐振子模型的量子化问题
2月6日12时,《张朝阳的物理课》第二十六期开播。搜狐创始人、董事局主席兼CEO张朝阳坐镇搜狐视频直播间,开讲谐振子模型的量子化问题。张朝阳先回顾经典力学中谐振子的运动方程、势能,再从双原子分子中两个原子间的势能出发,通过泰勒展开得到最低势能点附近的谐振子近似,以此阐述了谐振子在微观世界的普遍性,最后通过求解谐振子的薛定谔方程,带领网友成功理解谐振子模型的量子化问题。

文章插图
“人生的意义在于干活。”张朝阳在小白板上写下“虎年第二课”,同时为网友送上虎年祝福,他说,“干活需要学习,有了知识,才能更有效地干活。学物理,可以了解世界。”他也介绍,已有很多物理学家来搜狐视频开讲,“短视频时代,有心学习,除了看直播,还可反复看回放。”
回顾经典线性谐振子:胡克定律与运动方程张朝阳先带着网友回顾经典力学中的谐振子问题。以弹簧-小球模型为例,在经典力学中,谐振子的回复力是F=-kx,即所谓的胡克定律。根据牛顿第二运动定律,可以得到谐振子的运动方程:
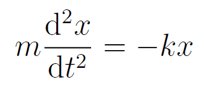
文章插图
他告诉网友,在通常的处理中,物理学家会通过定义角频率ω0=√(k/m)来简化符号的使用。他快速给出上述方程的解的形式:x=Re[x0 e^(iω0 t)]。他提醒说,“谐振子以正弦的形式振动,ω0是振动的角频率。”他也顺势介绍谐振子在振动过程中,动能和势能互相转化,总能量保持不变。在谐振子中,势能的微分du=-Fdx,于是得出谐振子的势能公式。
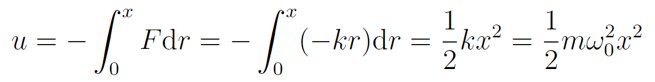
文章插图
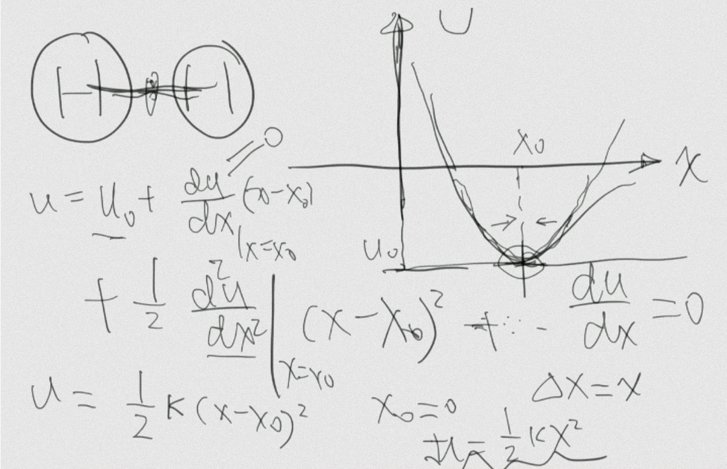
分子势能模型:选取平衡位置点 泰勒展开做近似谐振子是弹簧的理想模型,但是微观世界并没有弹簧,那么谐振子对于量子力学有什么意义呢?张朝阳以双原子分子为例,对此作出生动的介绍。他在小白板上明示双原子分子中的两个原子之间的势能。
文章插图
(双原子分子中的两个原子之间的势能曲线(右上角))
他说,“这个势能曲线有一个最低点。”从经典力学来看,当系统能量比较小时,双原子分子将会处在最低能处附近。而势能曲线在势能最低的形状恰好和抛物线类似,因此可以近似成谐振子。对此,张朝阳带着网友进行公式推导,主要方法来自于势能在能量最低点的泰勒展开:
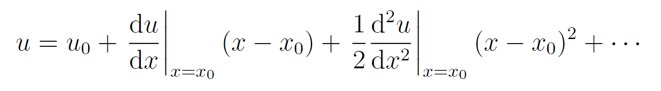
文章插图
他提醒网友,“省略号表示泰勒展开的高阶项,可忽略。”他还指出,在势能最低点,势能的一次导数为0,于是上式的一次项为0。把二阶导数记为k,重新定义势能零点和坐标原点,即可以把势能近似为谐振子势能的形式:
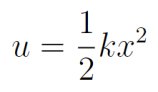
文章插图
“谐振子在物理中显得特别重要”,张朝阳强调了这个结论的普遍性。总的来说,只要是考虑势能极小值附近的微扰问题,都可以近似为谐振子。
求解薛定谔方程:谐振子能级与波函数提到谐振子的哈密顿算符,张朝阳再列公式做推导。
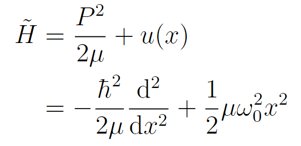
文章插图
“μ是等效质量”,他说,处理氢原子的时候由于质子比电子重很多,质子可以近似为在质心系中静止,因此哈密顿量可以直接用电子质量m。但是对于双原子分子,分子间的质量相差不大,哈密顿量里边的质量不能再直接使用其中某个原子的质量。
- 《张朝阳的物理课》探究谐振子模型的量子化问题
- 灯塔春节档报告:票冠《长津湖之水门桥》,延续“超级头部”格
- 本文转自:文汇客户端热不仅会扩散|再登《科学》!潘建伟团队首次测得神秘“第二声”衰减率,这种波动来自你天天接触的它……
- 名侦探柯南之《新干线大爆破事件》剧情解说新干线大爆破事件
- 一图读懂《防范和处置非法集资条例》
- 首批通过《净水机水效限定值及水效等级》,云米净水器有多强悍?
- 《咒怨》导演清水崇新作《牛首村》2段新预告 2月18日上映
- 《英雄联盟》“水晶先锋”斯卡纳终于要迎来重做
- 七绝《雪之怡情》
- 京东连续两年入选《财富》全球最受赞赏公司榜单 2022年行业榜
