一线城市|poisson和负二项回归

Poisson回归和负二项回归该如何分析
目录
1.前提条件1
2.分析流程图1
3.案例分析2
3.1背景2
3.2操作3
3.3SPSSAU输出结果3
3.3.1O检验3
3.3.2模型似然比检验3
3.3.3回归结果分析4
3.3.4模型预测4
3.4结论
1.前提条件
在分析之前，首先我们要了解Poisson分布和负二项回归分布的适用条件，它们均需满足以下三个条件：

文章插图

1.平稳性：发生频数的大小，只与单位大小有关系。(比如1万为单位，或者100万为单位时患癌症人数不同)
2.独立性：发生频数的大小，各个数之间没有影响关系，即频数数值彼此独立没有关联关系；比如前1小时闯红灯的人多了，第2小时闯红灯人数并不会受影响。
3.普通性：发生频数足够小，即低概率性。
2.分析流程图
不同的条件是Poisson回归要求等离散型，负二项回归分布不要求等离散性，这时我们可以运用SPSSAU采用O检验来判断数据更适合哪种回归进行分析；判断出合适的回归；接下来无论是Poisson回归还是负二项回归都需要对模型进行似然比检验，判断模型有效性；最后进行相应的回归分析，并对模型预测。流程图如下：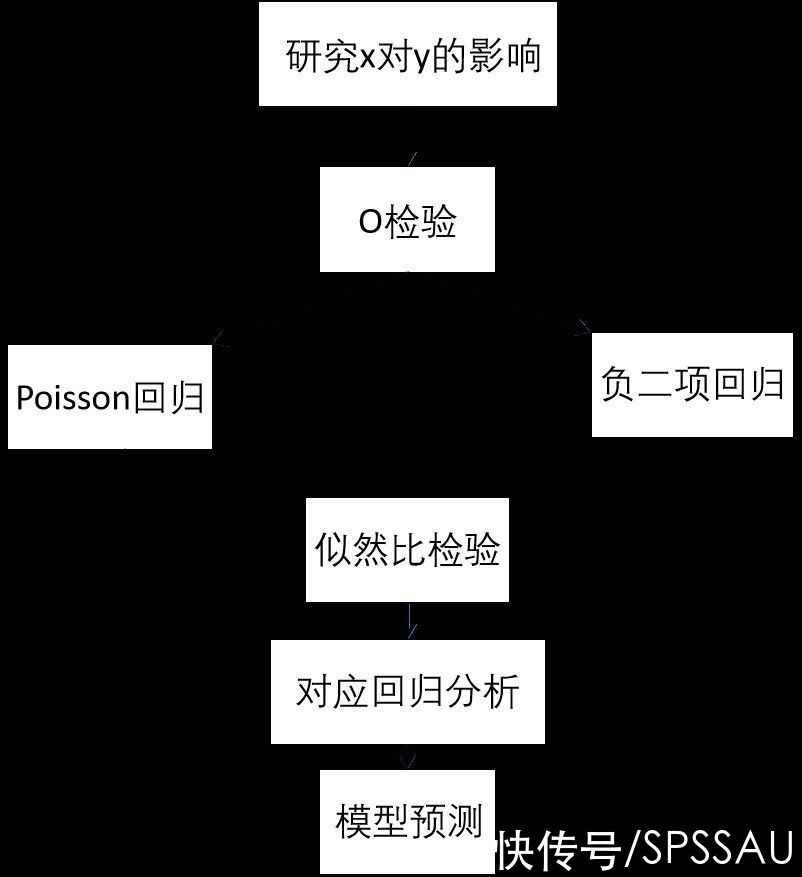

文章插图

分析流程图
3.案例分析
下面我们结合具体案例加以说明，案例如下：
3.1背景
当前有一项针对专利数量的影响关系研究，研究政府对于企业的支持力度，是否一线城市，对于企业专利数量的影响情况。共收集10个城市的数据，如下：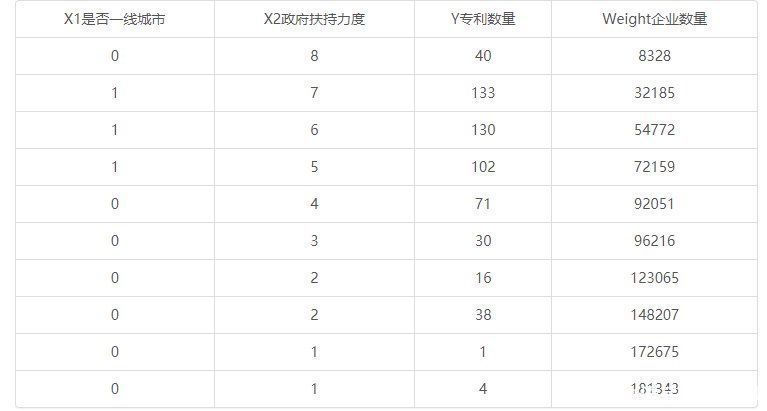

文章插图

其中在否是一线城市（x1）中，1表示是，0表示否；政府扶持力度（x2）中，各个数字数值大小表示政府扶持力度的大小。
3.2操作
本例子中专利数量是基于‘Weight企业数量’，因此‘基数Eposure【可选】’框中应该放入‘Weight企业数量’这项，因变量和自变量也放入对应位置。如下图：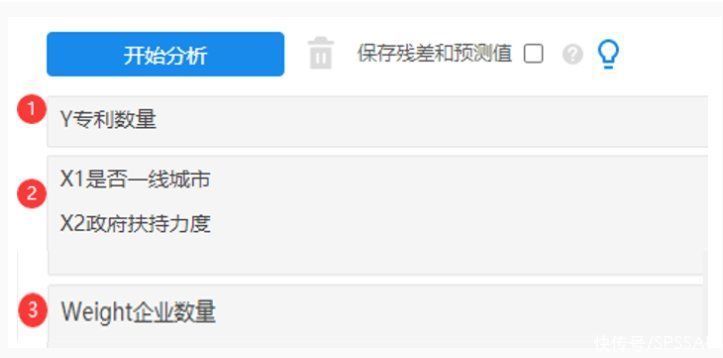

文章插图

3.3SPSSAU输出结果
3.3.1O检验
在SPSSAU中，可通过O检验（计算公式：）,其中n表示样本量，S表示事件方差，M表示事件平均值，O检验近似服从正态分布），以及平均值和方差的大小对比，综合判断是否存在过离散现象。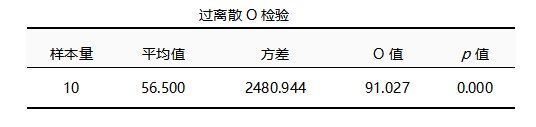

文章插图

根据O检验表可知，专利数量的平均值是56.500，方差是2480.944，明显平均值与方差不相等，存在过离散现象，而且O值明显大于1.96（p=0.000
3.3.2模型似然比检验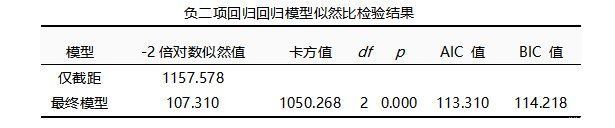

文章插图

第一：首先对p值进行分析，p值无限接近于0且小于0.05，则说明模型有效，可以进行负二项回归分析。
第二：AIC值和BIC值可用于多次分析模型时的对比；此两个值越低越好；如果多次进行分析，对比该两个值的变化情况，综合说明模型构建的优化过程；
3.3.3回归结果分析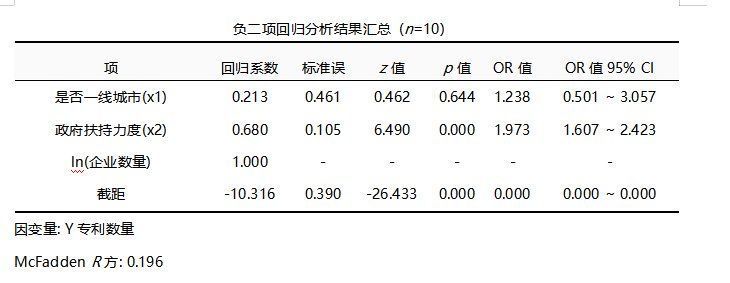

文章插图
从上表可知，将X1为是否一线城市,X2为政府扶持力度，共2项为自变量，而将Y专利数量作为因变量进行负二项回归分析，从上表可以看出，模型公式为：Log(Y)=-10.316+0.213*X1+0.680*X2+ln(企业数量）
X1是否一线城市的回归系数值为0.213，但是并没有呈现出显著性(z=0.462，p=0.644>0.05)，意味着X1是否一线城市并不会对Y专利数量产生影响关系，即城市类别与专利数量无明显关系。X2政府扶持力度的回归系数值为0.680，并且呈现出0.01水平的显著性(z=6.490，p=0.000