ETC|所有人的银行卡密码、生日和手机号都包含在圆周率中，是真的吗？域名|rw战队|Linux

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

圆周率是我们在小学时候已经接触过的一个数学常数，如果我们想要计算圆的周长、面积、以及球形的体积，就必须要用到圆周率这个概念。这是为什么呢？
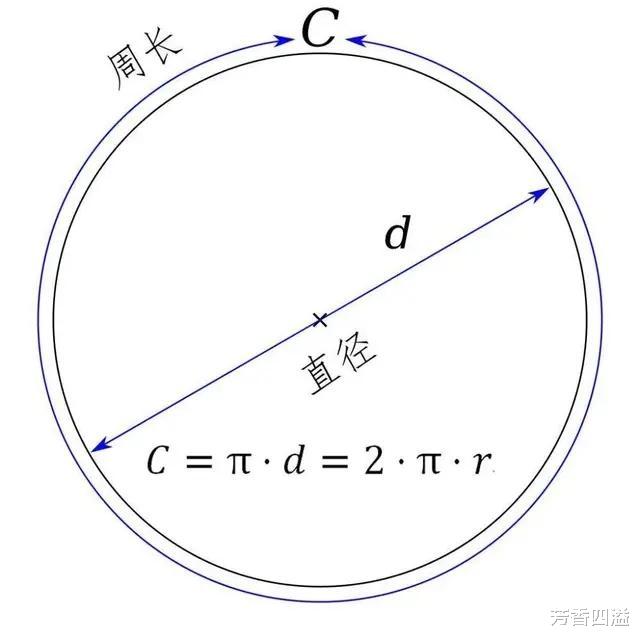
其实看了圆周率的定义就知道了，它是一个圆的周长和直径的比值，或者是一个圆的面积和半径平方的比值，用希腊字母π来表示。

古时候人们在求圆周率的时候，不管是大圆小圆都发现这个比值是一个常数，都是一样的，总是以3.1415...开头。
如果我们能精确的求出这个数字，那么反过来我们就能根据圆的半径准确的知道圆的周长和面积。这个怎么理解呢？

你看，一个直径为1的圆，那么它的周长就是圆周率，如果我们知道的圆周率越是准确，那么我们算出来的圆的周长就越准确。
这个规律均被当时全世界上各个地区、不同文化的数学家所发现，于是就开启了一场人类精确求解圆周率的过程。

圆周率看似简单，周长和直径的比值，但是人们在求解的过程中发现这个数字并非一个有限的数，越求越长，因此不能用分数简单的表示。
现在我们知道圆周率其实是一个无限不循环的小数，称为无理数，这也说明一个圆的周长也是一个无理数，也就是说组成圆的线段的长度并不是一个有限的数值，而是在无限的逼近一个数值。

所以说，我们所说的圆的周长、面积都是一个近似值，这也是为什么自然界、包括人类在内无法造出一个完美的正圆的原因。因为在理论上，要想精确的算出一个圆的周长和体积必须要将圆周率算尽。
不过对于生活来说，我们将圆周率取小数点后两位就可以了，完全可以满足精度的要求。精密工程以及物理学上对行星轨道的精确计算也只需要取值到小数点后十几位就可以了。

其实为了获得准确的圆周率数值，人类也是废了老大的劲，从几千年前就开始计算，我们比较熟悉的就是我国南北朝时期的祖冲之，继承了数学家刘徽的割圆术。
也就是在一个圆内外无限的内接和外界多边形，接的越多，多边形的周长就会无限的接近圆的周长，这其实就是我国早期求极限的思想。

祖冲之将圆周率精确到了小数点后7位，给出不足近似值3.1415926和过剩近似值3.1415927 。
古希腊的阿基米德也是计算圆周率的大师，他在死前的一刻还在计算圆周率，据说是一位罗马士兵冲进阿基米德的住宅，看见一位老头在地上画一些看不懂的符号，阿基米德严厉喝止这位士兵不要把他的圆弄坏了，士兵勃然大怒，将阿基米德斩杀，一代大师就这样死于刀下。

不过阿基米德生前还是将圆周率通过迭代算法和两侧数值逼近的概念，计算出圆周率的近似值为3.141851 。
不管是几何法还是后来的分析法，所计算的圆周率是远远不够的，而且已经到这人为手算的极限，随着现代计算机的出现圆周率才开始被大规模的推算，在1973年，我们就算到小数点后一百万位。