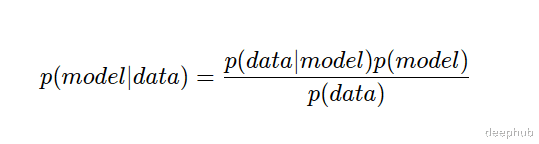
京东|数据为中心和模型为中心的AI只是贝叶斯论和频率论的另一种变体吗？客服

文章图片

从统计的角度对数据为中心和模型为中心的人工智能
五年前深度学习的一切都是关于如何构建新的、更优化的模型，以便更好地从非结构化数据中学习。这些努力带来了许多研究突破，突破了神经网络的可能性。但慢慢地越来越多的人对这种方法提出了批评，并建议首先关注数据的质量和一致性。这些批评的声音通常来自行业，来自在关键业务环境中长时间大规模操作模型的专业人士。
在这篇文章中，我将对这两种方法提供一个新的视角。我将从统计的角度来看它们，看看它是否可以阐明哪种方法更好以及在什么情况下更好。
统计学有两个学派——频率派和贝叶斯派——它们与我们的主题有着有趣的相似之处。

在频率派中寻找概率 p(data|model) ，这意味着我们“假设”数据， “知道”模型。换句话说，模型是确定的(至少在工作目的上) ，但我们的不确定的测量，即数据，可能或可能不完美地反映模型(甚至现实) 。
在贝叶斯方法中，我们寻找的概率是p(model|data) ，即我们“假设”模型， “知道”数据。我们的模型是不确定的，而数据是我们的基本事实——我们所知道的唯一确定的就是手头上的数据。

这些假设也导致了两种方法的不同重点。频繁主义者的方法涉及大量异常值、匹配方差和样本大小的概念，即它是以数据为中心的，不太关心模型。另一方面，贝叶斯方法是关于先验、可信度和抽样的，这意味着它们以模型为中心。为了理解这如何帮助我们更好的描述以模型为中心和以数据为中心的AI之间的区别，让我们先考虑一下统计学中最重要的方程:贝叶斯定理:

这意味着通过了解我们对模型（即 p(model) ）和数据（即 p(data) ）的确定性，我们可以合并这两个看似相反的观点。还有就是细节决定成败，这些无条件的概率在实践中会引起很多问题，我们下面继续讨论
归纳偏差和以模型为中心的AI我们取p(model) ，它是一个特定模型拟合未来数据点的概率。如果它很高，那意味着我们相信有一个很好的数据模型。最大化这个概率的一个策略是在模型中加入一些归纳偏差。归纳偏差基本上是研究者关于问题空间的先验知识的某种升华。这就是为什么在以模型为中心的AI中我们喜欢:

引入受生物启发的架构(例如卷积滤波器)
定义复杂/复合损失函数(例如感知损失)
在超参数的可行范围内尝试网格/随机搜索

这些实际上是非常强大的方法。但这里有一个很大的问题:归纳偏差（不管它是否有用）仍然是一种偏差。
当选择一个特定的架构时，也限制了从数据中学到的东西。但是我们有时是喜欢这样做的，因为：
(1)我们知道数据中有某种噪声(即任务无关方差)和/或
(2)我们没有足够的数据来学习任何任意函数。
所以我们提出了两种主要的缓解措施:
(1)添加更多的数据，这样就可以训练更复杂的模型。
(2)将问题分解成步骤，并为它们训练单独的模型。
研究人员观察到的一件重要的事情是，添加的数据越多所需的归纳偏差就越少。例如，对试图学习的领域， transformer只需要很小的归纳偏差，但是却需要更大的数据（还记得VIT吗）。实际上，我们总是希望尽可能少地使用归纳偏差，因为我们希望AI系统解决的大多数任务都不容易创建先验模型(想象一下围棋或蛋白质折叠) 。当我们没有正确的模型架构来完成任务时，无论如何高效地寻找超参数，都将以低于标准的性能结束。